| タイトル | 新課程 チャート式基礎と演習数学 数学IA 数学IIB 数学III 数学C | |||||||||||
| 出版社 | 数研出版 | |||||||||||
| 出版年 | 2022/02 | |||||||||||
| 著者 | チャート研究所 | |||||||||||
| 目的 | 教科書基礎~入試基礎・インプット型 | |||||||||||
| 対象 | 現役生から大人の学び直しまで(全統模試偏差値55程度まで) | |||||||||||
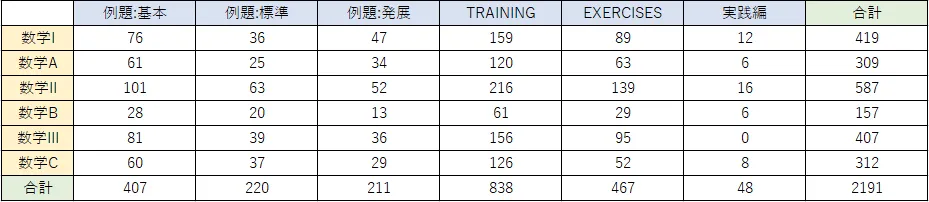
| 分量 | 数学IA+IIB+IIIC(例題+TRAINING+EXECISE+実践)2191題 | |||||||||||
| 評価 | ||||||||||||
| AI | 同じ論点の難しい問題を生成 | |||||||||||
| レベル | 日常学習 | 教科書基礎 | 教科書標準 | 入試基礎 | 入試標準 | 入試発展 | ||||||
※入試基礎=日東駒専、地方国公立 入試標準=MARCH、関関同立、準難関国公立(地方医含む) 入試発展=旧帝大上位、早慶、医学部
加筆修正の履歴
2026/02/28 白チャートの接続先を全体的に書き直しました。
2026/02/24 大人の学び直しとしての評価を追記しました。
2026/02/16 白チャートの接続先に『数学の良問問題集』を加えました。
2026/02/15 白チャートの接続先の読みにくい箇所を書き直しました。
2026/02/13 白チャートの接続先を全体的に書き直しました。
2026/02/11 白チャートの使い方で使用する問題集の一部を変更しました。
2026/02/08 改訂版情報に追記しました。
2025/11/04 使用開始時期・問題数に部分利用を追記しました。
2025/11/03「チャート式の使い方」の復習を例題のみに強調し、「白チャートの接続先」を全体的に読みやすいように修正しました。
2025/11/01 白チャートの接続先の内容とチャート式の使い方「STEP2」の内容を一部修正しました。
2025/10/31 『入門問題精講→黄or青チャート』→『入門問題精講→青チャート』に変更しました。チャート式の使い方「STEP2」の内容を一部変更しました。
2025/10/26 白チャートの接続先として挙げた「1対1対応の演習」の例題のみに取り組むことを追記。
基礎固めなら白チャート
本書は数研出版から出版されている非常に有名な数学の参考書です。入試数学の網羅的対策を行うならチャート式の名前を聞いたことがない人はいないでしょう。本書はそのシリーズの「白」にあたります。本書シリーズには「白・黄・青・赤」と4種類があり、特に「青」は自称進学校から全国有数の進学校まで幅広い場所で配布されることもあって有名です。数研出版は数学の教科書での採用率も高く、また物理や化学、生物などの理科科目では『重要問題集』が受験生の間ではよく採用されています。数理科目なら数研出版と言っても過言ではない信頼と安心があります。
本書シリーズの「白・黄・青・赤」の4種類は難易度別に分かれており、「白」は最も易しい位置づけです。チャート式シリーズはどれも基本例題から始まるため、最も難しい「赤」であっても例題自体はそこまで難しくありません。そのため、白よりも難しい位置づけにある「黄」や「青」であっても基礎固めとして用いられることがあります。しかし、もともとチャート式は基本問題を備える教科書や教科書傍用問題集と棲み分けた位置づけにあるため、本当の意味での基礎固めとしては問題数が足りずに十分には機能しません。
その点で本書「白」は特殊な位置づけにあり、チャート式シリーズの中では唯一基礎固めとして正しく機能します。というのも、本書の基本例題は教科書基礎レベルの素直な問題から始まり、その上でチャート式らしい大量の演習を行えるからです。その他の「黄」や「青」は基礎固めというより、いわゆる解法暗記を地で行く参考書になっていると考えた方が誤解が少ないと思います。高校数学の基本計算や解法を身につけることを意図する「白」に対して、入試を強く意識する「黄」と「青」というイメージです。
多くの受験生が白で十分な理由
文系理系によって違いはあるものの、多くの受験生は「白」から取り組むのがベストと考えます。チャート式シリーズで最も有名な「青」は主に入試基礎~標準を網羅する参考書なので、基本例題の簡単さに釣られて取り組むと痛い目に遭います。「黄」や「青」の基本例題は意外と変化球が多め。最初から「青」に取り組める人とは、教科書レベルならほとんど問題がないと言える人、かつ難関大理系志望と考えて良いと思います。
それ以外は教科書の復習が必須ですから、となると「白」で基礎固めをしてから受験戦略を立てていく方が良いでしょう。中学生や高校1年生の先取りとしても「白」が無難です。なぜ、ここまで「白」にこだわるのかというと、数学は基礎固めが非常に重要なため、中途半端に入試対策の解法暗記に取り組むと「問題と解答の丸暗記」に陥って応用が利かなくなるからです。挙句に挫折してしまうと捧げた時間の多くを無駄にします。それを防ぐには“ここまでならできる”という土台を着実に大きくしていくことです。
チャート式参考書 レベル表 https://www.chart.co.jp/goods/item/sugaku/level/level3.html
こちらは公式サイトで提供されているレベル表ですが、実際には同じ例題を見比べても「白」と「青」では大きく異なります。白の場合、定理や公式も例題として扱い、数学が苦手な人にも配慮した易しい問題構成となっている=基礎固めを重視しているのに対して、教科書との重複を避ける「青」に関してはすでにそうしたものがわかっている前提で構成されています。押さえておくべき基本を正しくイメージできるのは「白」です。
これらを考慮した上で改めてレベル表を調整すると以下のようになります。
| 青 | 教科書基礎 | 教科書標準 | 入試基礎 | 入試標準 | 入試発展 | |||||||
| 黄 | 教科書基礎 | 教科書標準 | 入試基礎 | 入試標準 | 入試発展 | |||||||
| 白 | 教科書基礎 | 教科書標準 | 入試基礎 | 入試標準 | 入試発展 | |||||||
チャート式に取り組む理由の一つには、大量の問題を解くことによって自分自身の当たり前のレベルを上げることにあります。英語で言うと、単語を見た瞬間に理解できないと問題を解くことすらままならないですよね。いくら簡単な問題であっても解くことに時間がかかってしまうと、時間制限のある試験ならなおのこと、それよりも難しい問題を解く際には考えたい論点まで辿り着かないわけです。加えて、応用問題を基礎的な知識に分解できないと、応用問題に取り組む意味も希薄になります。
では、どれほどの問題数を解くべきか。これには様々な議論がありますが、少なくとも基礎部分ほど当たり前にする必要がある、すなわち白チャートの問題数に限っては否定されにくいと思います。率直に理にかなった参考書です。もちろん、高校偏差値65以上の進学校に通い、学習塾などで中学時代から大量の問題を解いていたような人にはチャート式の問題数は過剰に働く可能性があります。この場合なら「青」に一通り目を通して、わからない問題の解法だけ器用に暗記すれば良いでしょう。
使用開始時期・問題数
チャート式の問題数はかなり多いため、網羅的に取り組むなら使用開始時期は当然考えなければなりません。遅い時期から取り組んで1周もできないくらいなら、もっと問題数の少ない『入門・基礎問題精講』や『Super Quick 数学』『文系の数学 重要事項完全習得編 改訂版』に取り組んで少しでも周回するべきです。中学生と高校1年生の先取りならいつでも可能、受験勉強として取り組むなら遅くとも高校2年生夏休み開始までには取り組みたいところです。
ただ、チャート式は難易度(コンパス)から部分利用もしやすいので、教科書基礎レベル(コンパス1~2)だけ器用に取り組むこともできます。目当ての参考書に接続する前の基礎知識の調整として使える点も、正しく教科書基礎から始まっている白チャートの利点だと思います。それに白チャートのコンパス1~2が完璧に解けなければ入試数学は全く先に進めないどころか、背伸びした参考書に手を伸ばした結果、実力にならずに時間を無駄にする恐れまであります。
※『文系の数学 重要事項完全習得編 改訂版』も優れた参考書なので、以下の記事も参考にして自分に合った方針と問題数を考えてみてください。
また、「黄」や「青」の場合は問題の取捨選択が重要になる場合もありますが、教科書基礎から始まる「白」なら難しく考えずに片っ端から解いてしまっても良いと思います。これだけ解けば呼吸をするように基本問題は解けるようになるので、入試基礎以降の積み重ねを効率的に行えます。さらに言うと、本番の試験でも絶対に解かなければいけない問題を解ける心理的な利点は大きなもので、もし「黄」や「青」に取り組んで基本問題を落とした上に、発展問題もいまひとつ解けないといった事態になったときの精神的なダメージは受験結果を左右しかねません。
チャート式の使い方―過去問分析を終えたあと
1周目は例題(基本・標準・発展)を解きます。基本の基本問題は言われるがままに解くだけで十分ですが、解法が覚えにくい問題は自分なりにポイントを考えておきます。また、1周目は「どこのページにどんな問題があったのか」を把握することも重要です。本書を終えたあと、別の参考書との往復で何度も確認します。
『新課程 チャート式 基礎と演習数学I+A 基本・標準例題完成ノートパック』—例題の周回に便利なアイテム
1周目の例題を終えたあとはTRAINING・EXERCISESに取り組み、例題の知識の定着を図りながら演習量を稼ぎます。その後は入試基礎以降の問題集に取り組みながら適宜復習します。使用する問題集は第一に現在の実力に最も近い『併願校の過去問』です。
過去問だけだと問題数が足りないと思うので、国公立志望なら『短期攻略 大学入学共通テスト 数学Ⅰ・A基礎編』でマークシート対策を兼ねます。私立志望なら『文系の数学 重要事項完全習得編 改訂版』で白チャートの網羅的な知識を重要事項に絞ってブラッシュアップします(演習題はアウトプットに最適)。より難易度の高い『1対1対応の演習』を取り入れるのもありです。さらにアウトプットを意識して『新数学スタンダード演習(A・B問題)』にチャレンジしても問題はありません。
※1対1対応の演習と文系の数学はハイブリッド型です。これらは完全なアウトプット型ではないからこそ、白チャートよりも難しい入試基礎~標準の問題に接続しやすいと思います。
※『短期攻略 大学入学共通テスト 数学Ⅰ・A基礎編』シリーズは国公立志望なら優先して取り入れます。さらに演習量を稼ぐために“実戦編”まで使用しても問題ありません。他の出版社の共通テスト問題集でも可。
「STEP.1」と「STEP.2」を経て、白チャートの知識をどのように整理すれば良いのか、応用問題に活用できるのかなど得点に最適な考え方に気づき始めていると思います。そういった点を押さえながら、自分自身に教えるように「例題」を復習します。1周目は最初から最後まで手を動かして解きますが、2周目以降は問題を見た瞬間に解答が思い浮かばないものと苦手問題だけに絞ります。最終的には手を動かさずに英単語のように「問題→解答」を頭の中に思い浮かべるだけです。
STEP.2で使用した問題集(過去問以外)をメインに使用します。できるだけ早くアウトプット中心にするのが有力。もちろん、チャート式のインプットをできるだけ正確に行うに越したことはありませんが、今はAIによって多少力が足りなくともアウトプットの質は高められます。
チャート式の欠点は膨大な問題数によって悪しき解法暗記に陥り、全く応用力がつかないことにあります。この欠点を解消するには、最初からアウトプットを想定することです。チャート式を何周もするのではなく、アウトプットからインプットの重要性に気づき、一刻も早くチャート式の本当の使い方を理解すること。でなければ、チャート式の問題を解いて満足しているだけになります。
白チャートの問題は完璧になったのに、本番の問題が解けないとき
チャート式の問題と解答が瞬時に頭の中に思い浮かび、単元ごとの問題の種類や解法も一通り把握しているのに本番の問題が解けないことがあるかもしれません。難しすぎる問題は当然解けないとしても、難易度からして解けるはずの問題が解けない場合は問題の意図と知識の引き出し方がわかっていないためと思われます。
チャート式のようなインプット型の参考書は単元ごとに分けられていることもあって「問題の意図を掴むこと」が簡単です。言われるがまま解法を適用すれば解けてしまいます。しかし、本番はランダム出題で問題の意図を把握するところから考えなければなりません。問題は何を要求しているのか。どの解法を適用すれば良いのか。このわかりやすい解決方法は「アウトプット型問題集」に取り組むことです。すぐに答えを見ずに自分の手札(チャート式で得られた知識)から答えまでの道筋を考え抜きます。
そして、そういった作業を何度も繰り返していくと、問題と解法の分類がどんどん進みます。適切なアウトプットが高い学習効果を生むのは、ある意味で不自由が思考力を育てる、全身運動のように普段使っていない頭の筋肉を刺激するからです。さらにアウトプットは逆算思考を強化し、効率の良いインプットにも繋がります。「きっとこういう問題が出てくるだろう、だからここを要点として覚えておこう」と予測できるようにもなるわけです。こういった経験が少ないうちは覚え方に無駄が多く、覚えたものの応用を考えられないのは仕方ありません。誰しも一度は通る道です。
白チャートの接続先は?文系と理系ごとに紹介
まず、文系志望が白チャートのあとに取り組む参考書には2つの方針があります。1つは解法暗記の継続。難関大志望がさらなる解法暗記によって網羅度を高める場合、白チャートが教科書基礎~入試基礎までなので、難易度から入試基礎~標準までを扱う『1対1対応の演習』に接続するのがベストです。文系は最難関大を除くと典型問題の出題率が高いため、理系ほどアウトプットにこだわる必要がありません。
次に、成成明学・MARCH・関関同立・地方~中堅国公立志望なら『数学の良問問題集』への接続もオススメです。『数学の良問問題集』は入試基礎~標準までの典型問題を集めたアウトプット型問題集。「確認問題」で白チャートまでの知識を復習でき、「必須問題」で大学偏差値50~60くらいの問題に挑戦できます。「レベルアップ問題」は入試標準~やや難(60~65)なので、志望校によって難化対策でもなければ取り組む必要はありません。
さらにおまけでもう1つ『新数学スタンダード演習(以下スタ演)』に取り組む方針もありと言えばありだと思います。数学がそれなりに得意であることが条件ですが、『1対1対応の演習』よりも全体的にやや難しいアウトプット型問題集なので使いこなせたときには最も実力が伸びます。ただし、白チャートの基本的な知識と解法に分解・帰着できないと意味がありません。青チャートとの併用によって無理やり使いこなせなくはないと思いますが、その方法を選ぶ人はなかなかいないでしょう。やってみる価値はあるものの、難しいと感じたら無理する必要はありません。
理系志望の場合、中堅私大や地方国公立のような入試基礎までの典型問題しか出題されない大学なら白チャートの基礎固めはちょうど良いのですが、難関大志望は数学IIICまでの量を考えるとアウトプット中心の方針で実戦的な解法暗記を優先したい事情があります。つまり、かなり早い時期から取り組める場合を除いて、白チャートによる基礎固めはオススメできません。基礎固めするにしても『数学入門問題精講』のような問題数を抑えた参考書にするか、学校の授業で教科書レベル(コンパス1~3)は理解している前提で『文系の数学 重要事項完全習得編』や『1対1対応の演習(例題)』から取り組むのが現実的だと思います。
では、かなり早い時期から白チャートに取り組んでいた場合の接続先は何がオススメか。これもほとんど文系と同じ理由で『1対1対応の演習』や『スタ演』がオススメですが、もう1つ発展的に『解法のセオリー』も挙げられます。これはすぐに接続するわけではないのですが、理系は文系よりも量が多いため、単純な解法暗記だけでは収拾がつかなくなります。ひとつひとつの知識からの抽象化と応用の検討が増えるということ。その気づきを得やすい参考書が『解法のセオリー』になっています。これ以外にも理解を深める参考書は文系以上に必要になりますし、『プレックス数学重要公式・定理集』で公式・定理を丁寧に確認しながら解く習慣も推奨されます。開始時点の実力や時期によって結論は大きく変わりますが、理系は単純な解法暗記ではなく、実戦を通じた解法暗記とも言うべき方針で入試基礎~標準までにどれほど時間を注げるかが受験戦略としては重要だと思います。
大人の学び直しとしての評価
白チャートを使って学び直す選択はとても良いと思います。特に現役時代に入試で数学を選択していなかったり、数学が苦手だったという人にとっては程良い難易度、かつチャート式らしく様々な問題と解法に触れられますから学びは多くあります。親の立場であれば、高校数学の大変さをこれほどわかりやすく理解できる参考書はないかもしれません。また、数学はパズル的に問題を解く楽しさを体験しやすく、普段の生活における思考力も向上する期待が大きく持てる科目です。言ってしまえば、世の中の多くの人は直感的な選択が中心ですから、数学の問題を解く際のあのじっくりと考える時間は力になるのです。
















